PSNR
The most prominent method is the PSNR (peaked signal-to-noise ratio). It is based on the idea, that the reproduced image consists of the original plus a "noise signal". The noise level can be characterized by the signal-to-noise ratio and is usually given in dB. Values below 0 dB mean that the noise power is larger than the signal. For identical images (zero noise), the PSNR is infinite.
Advantage is, that it's a well established method and the calculation is extremely simple (see here for the formula). Disadvantage is, that it is a purely mathematical calculation of the noise power, while the human psychovisual system is completely ignored.
Thus, one can easily to make 2 images, which have different types of compression artifacts (i.e. from different codecs) and have the similar PSNR compared to the original. But one looks much better than the other. Therefore, current opinion among specialists is, that PSNR can be used or optimizing one codec, while it fails for comparing different codecs. Unfortunately, many codec comparisons in the internet still use PSNR.
SSIM
SSIM (structural similarity) was fist suggested by Zhou Wang et.al. in the paper "Image Quality Assessment: From Error Visibility to Structural Similarity" (IEEE Transactions on image processing, Vol. 13, No. 4, April 2004, PDF).
The paper is very well written and I recommend anyone, who is interested, to read it. In short: The structural similarity is composed of 3 values:
- Luminance comparison
- Contrast comparison
- Structure comparison
A difference to PSNR is, that the SSIM index for a pixel is calculated by taking the surrounding pixels into account. It calculates some characteristic numbers known from statistics: The mean value, the standard deviation and correlation coefficient.
One problem with the SSIM is, that the algorithm has some free parameters, which are slightly different in each implementation. Therefore you should be careful when comparing your results with numbers coming from a different routine. I took the parameters from the original paper, i.e. K1 = 0.01, K2 = 0.03 and an 11x11 Gaussian window with a standard deviation of 1.5 pixels.
Implementations
Both methods are available in gavl (SSIM only in CVS for now), but their APIs are slightly different. To calculate the PSNR, use:
void gavl_video_frame_psnr(double * psnr,
const gavl_video_frame_t * src1,
const gavl_video_frame_t * src2,
const gavl_video_format_t * format);
src1, src2 and format arguments are obvious. The result (already in dB) is returned in psnr for each component. The order is RGB(A), Y'CbCr(A) or Gray(A) depending on the pixelformat. PSNR can be calculated for all pixelformats, but usually one will use a Y'CbCr format and take only the value for the Y' component. In all my tests the PSNR values for chrominance were much higher, so the luminance PSNR is the most pessimistic (i.e. most honest) value.For SSIM you can use:
int gavl_video_frame_ssim(const gavl_video_frame_t * src1,
const gavl_video_frame_t * src2,
gavl_video_frame_t * dst,
const gavl_video_format_t * format);
src1, src2 and format are the same as for PSNR. The pixelformat however must be GAVL_GRAY_FLOAT, implying that only the luminance is taken into account. This decision was made after the experiences with PSNR. The SSIM indices for each pixel is then returned in dst, which must be created with the same format. The MSSIM (mean SSIM) for the whole image can then be obtained by averaging the SSIM values over all pixels. The function returns 1 if the SSIM could be calculated or 0 if the pixelformat was not GAVL_GRAY_FLOAT or the image is smaller than the 11x11 window.It never matters which image is passed in
src1 and which in src2 because both algorithms are symmetric.Example
Below you see 11 Lena images compressed with libjpeg at quality levels from 0 to 100 along with their PSNR, SSIM and file size:
Quality: 0, PSNR: 23.54 dB, SSIM: 0.6464, Size: 2819 bytes
Quality: 10, PSNR: 29.84 dB, SSIM: 0.8473, Size: 4305 bytes
Quality: 20, PSNR: 32.74 dB, SSIM: 0.9084, Size: 5890 bytes
Quality: 30, PSNR: 34.38 dB, SSIM: 0.9331, Size: 7376 bytes
Quality: 40, PSNR: 35.44 dB, SSIM: 0.9460, Size: 8590 bytes
Quality: 50, PSNR: 36.31 dB, SSIM: 0.9549, Size: 9777 bytes
Quality: 60, PSNR: 37.16 dB, SSIM: 0.9612, Size: 11101 bytes
Quality: 70, PSNR: 38.34 dB, SSIM: 0.9688, Size: 13034 bytes
Quality: 80, PSNR: 40.00 dB, SSIM: 0.9768, Size: 16410 bytes
Quality: 90, PSNR: 43.06 dB, SSIM: 0.9863, Size: 24308 bytes
Quality: 100, PSNR: 58.44 dB, SSIM: 0.9993, Size: 94169 bytes
With these numbers I made a plot, which shows the PSNR and SSIM as a function of the JPEG quality:
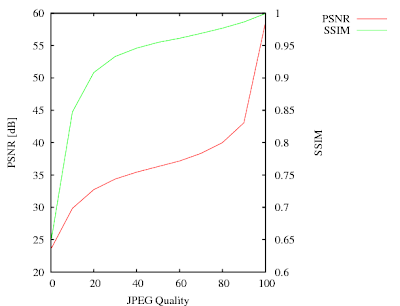The JPEGs have the most visible differences for qualities between 0 and 40. In this range the SSIM curve has the largest gradient. Above 40 (where the visual quality doesn't change much), the SSIM becomes more or less linear and reaches almost 1 for the best quality.The PSNR curve is a bit misleading. It has the steepest gradient for the highest quality. This is understandable because PSNR would become infinite for the lossless (perfect quality) case. It has however not much to do with the subjective impression. PSNR however is better for fine-tuning codecs at very high quality levels. That's because the PSNR values will change more strongly, while SSIM will always be almost one.
Now I have the proper tools to make a comparison of different video codecs.
Posts
No comments:
Post a Comment